Calculation Method for Qiblah Angle

Calculation Method for Qiblah Angle

Qiblah angle is calculated by using spherical trigonometry. i.e. by solving the equations for a spherical triangle

formed by 3 points : 1-The location of the praying person, 2- Mecca Al-Mukarramah and 3-The True North Pole.

Thus the vertices of this triangle will be arcs.

Now the shortest arc between the Praying person and Mecca lies on what is known as a Great Circle. i.e. a circle

whose plane cuts the Earth in two halves, thus passing into the Earth's Center.

The angle that this curve(shortest distance) make with the True North is the Qiblah Angle in question that needs to

be computed.

In the following example we are going to calculate the Qiblah Angle by which the Praying person should be facing

Mecca ; The Praying person will be in Montreal, Canada

What we need to know is two things: 1- the Geographical Co-ordinates(Latitude and Longitude ) for both Montreal

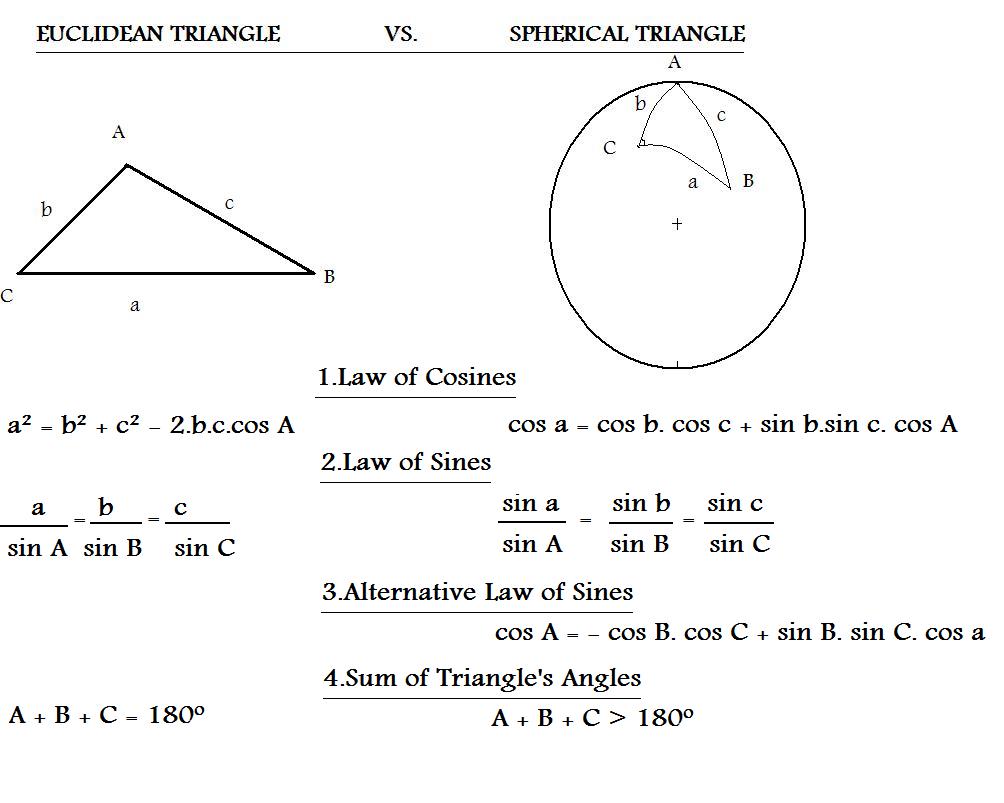
and Mecca, 2-The spherical triangle equations ( Laws of Sine and Cosine) which are shown in the diagram below:

In the diagram above C represents the Qiblah angle required where Montreal is located, point C.

At point B is Mecca and at point A lies the North Pole.

For Montreal : Latitude = 45.52 N and Longitude = 73.57 W

For Mecca:   Latitude = 21.26 N and Longitude = 39.49 E

STEP 1: Calculate angle a , the angle that the Praying person and Mecca's perpendiculars make

at the center of the Earth (look at the diagram):

From the top left diagram on the Earth sphere, that b and c are the complementary of the Latitudes of Montreal & Mecca

and also notice that angle A at the North is equal to the difference in Longitudes (in this case addition for East and West):

b = 90 - 45.52 ===> cos b = sin 45.52 & sin b = cos 45.52

c = 90 - 21.26 ===> cos c = sin 21.26 & sin c = cos 21.26

and by using the Law of Cosines, we find:

cos a = cos b. cos c + sin b .sin c. cos A

cos a = sin 45.52 . sin 21.26 + cos 45.52.cos 21.26.cos(73.57+39.49)

cos a =0.002946

==> a = 89.83 degrees ( at the center of the Earth).

STEP 2:

Using the Law of Sines, we get:

sin C = sin c. [sin A / sin a ] = cos 21.26 .[ sin 113.06 / sin 89.83 ] = 0.8575

==> C = 59 degrees.

Please note that in some cases you need to take the inverse of (180 -C) since

sin C = sin(180 -C), and you can verify that by using the Alternative Law of Sines.

STEP 3: If you need to calculate the shortest distance (and you can apply that for any 2 cities)

Multiply angle " a" from STEP 1 by 60 :

Distance = 89.83 * 60 = 5389.8 Nautical Miles.

Since the Earth is an Ellipsoid(not perfectly round ), a Nautical mile will be variant.

In US, one Nautical mile = 1.852 km , while in UK = 1.853 km.

thus, shortest Distance = 5389.8 * 1.852 = 9981.91 Kms.

NOTE: when we get closer to Mecca, then the Euclidean triangle equations might be easier to

apply, and it wouldn't have huge differences with the spherical triangle (Great Circle) method.

---------END of CALCULATION--------------------------------------------------------------------------